f(x)在x0点导数存在表示导数不是一个无穷大

 

 

1.函数图象在x0点的切线不垂直于x轴

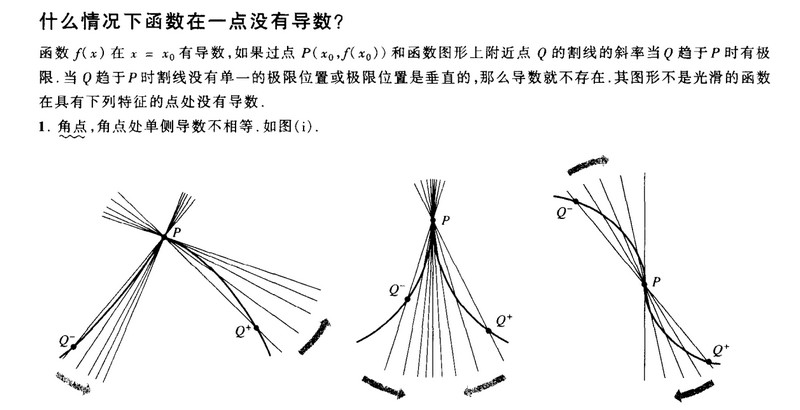
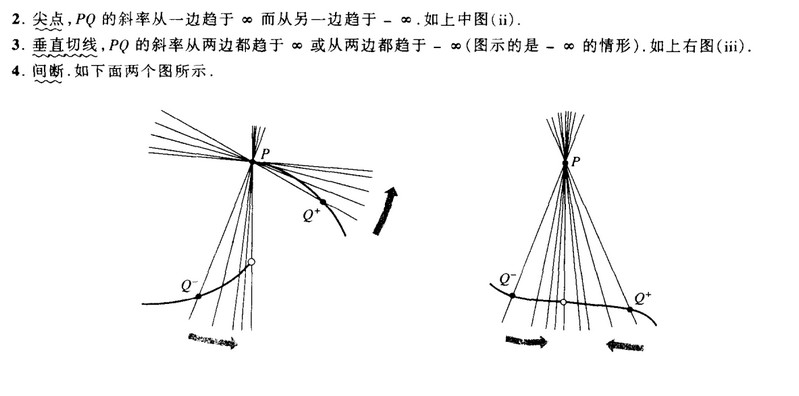
2.尖点--两边导数是正负无穷大

3.折点--两边导数不一样（如|x|在x=0）

4.间断两 两边的导数是正负无穷大

函数连续的充要条件是:函数在c点的左右的函数极限存在并且等于f(c)。注意这里是函数极限

lim_(x->c)f(x)=f(c)

函数的在c点可导或者在c点左右可导那么函数在c点一定连续

注意如果函数在c点不可导，那么函数在c点有可能还是连续的，看上面图iii --垂直切线那张

注意，上面的证明表示在c点导数存在(左右)并等于L，那么函数一定连续的。

如果左右导数存在但不相等，那么证明只要将上面的极限分成左右，取L1(左极限）L2右极限 (可以L1<>L2)，函数还是连续的

因为可以得出lim_(x->c+)f(x)=f(c)； lim_(x->c-)f(x)=f(c)。考虑尖角的情况f(x)=|x|在x=0点

 

上面f'(c)*0 因为f'(c)存在(不是无穷大)，所以f'(c)*0=0

 

 关于分段函数